回到学校, 没有mac, 没有reeder, 刷GR变成一件不能忍受的事了. 虽然chrome上有个非官方的reeder插件, 但是我们firefox党是有底线的啊啊啊! 遂心血来潮调教一下GR娘, 文字瘦身行距加大背景换换颜色之类的. 之所以用stylish而不是油猴, 是因为后者是js的而stylish只用写写css就好了. 折腾时多亏了firefox的自带的查看工具和firebug. 我觉得效果还可以:
代码在gist上, 注释良好.
update: 一段时间的使用和修改后, 放到 userstyles.org 上了, 可在此直接安装: http://userstyles.org/styles/68750/reeeder
整理自algo-class的ppt: note1 note2
参考资料:
Mathematics for Computer Science by Lehman & Leighton
Wikibook on Discrete Probability
样本空间 Ω = "所有可能的情况"
每一种结果 i ∈ Ω, 都有对应的概率 p(i) ≥ 0
样本空间概率和为1:
∑p(i) = 1 for i ∈ Ω
事件是样本空间的子集 S ⊆ Ω
事件的概率的定义:
∑p(i) for i ∈ S
随机变量 X 是一个函数:
X: Ω → ℝ
期望的定义:
随机变量 X 的期望 E[X] = 随机变量 X 的平均值
=∑ X(i)·p(i) for i ∈ Ω
期望的性质:
若 X1,...,Xn 是定义在 Ω 上的随机变量, 则
E[∑Xi] = ∑[E[Xi]]
(即使 Xi 不独立也成立! 但乘法不一样, 见下)
若 X,Y ⊆ Ω 是事件:
那么条件概率"Y发生下X发生的概率"的定义为:
Pr[X|Y] = Pr[X∩Y] / Pr[Y]
事件独立性的定义:
事件 X,Y ⊆ Ω 是独立的 ⇔ Pr[X∩Y] = Pr[X]·Pr[Y]
根据条件概率的定义:
上面那个成立 ⇔ Pr[X|Y] = Pr[X] ⇔ Pr[Y|X] = Pr[Y]
警告: 不要相信直觉...
随机变量的独立性的定义:
定义在 Ω 上的随机变量 A, B 是独立的 ⇔
事件 Pr[A=a], Pr[B=b] 是独立的, 对于所有的 a b
(⇔ Pr[A=a and B=b] = Pr[A=a]·Pr[B=b] )
如果随机变量 A, B 独立才有:
E[A·B] = E[A]·E[B]
警告: 不要相信直觉...相关的变量也可能独立...
引子——括号匹配问题
2n 个'('和')'组成的括号序列, 有多少种合法的组合方法?
把括号从 0 到 2n-1 编号, 合法的序列第 0 个一定是 '(' , 假设第 0 个括号与第 k 个括号匹配, 则序列 [1 ... k-1] 和 [k+1 ... 2n-1] 应也是合法的括号序列, 所以 k 必须是奇数, 设 k=2i+1 , 得公式:
如果换种说法, n 对括号的序列, 可得更简单的公式:
进一步证明
如果 '(' 看做是入栈, ')' 看做是出栈, 则 2n 个括号的合法序列, 一一对应于 2n 步合法的入栈出栈序列.
n 步入栈 n 步出栈的序列总数为 . 对于一个不合法的序列, 一定会在某一步(设为 2i+1 )发现此时遇到的出栈符号数多于入栈符号数, 即遇到了 i 个 '(' 和 i+1 个 ')'. 此时后面还有 n-i 个 '(' 和 n-i-1 个 ')', 如果将后面的 '(' ')' 互换则得到 n-1 步入栈 n+1 步出栈的序列, wikipedia 上说, 两者是一一对应的, 即一个不合法的 n 入 n 出序列(我擦我XE了), 一一对应了一个 n-1 入 n+1 出的序列. 所以可得公式:
化简得方便的计算公式:
应用
有一大票的问题可以归约到卡特兰数上, 看书也经常会看到把这个当做公式用在和式相关的证明中. wikipedia 上说某书列了66个可以归约到卡特兰数的问题(orz). 一般问题要么可以归约到括号匹配问题, 要么可以归约到入栈出栈问题, 比如:
把每一个字符绘制到一个小的区域中, 然后计算整个区域中的灰白比例, 得到对应的一个参数, 按参数排列得到一个字符按疏密排序后的列表.
import Image, ImageDraw, ImageFont
from itertools import product
def get_data_list():
fontpath = '/usr/share/fonts/TTF/DejaVuSansMono.ttf'
fontsize = 20
h = 24
w = int(h*0.618)
charlist = r'''0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ`~!@#$%^&*()-_=+[{]}\|;:'",<.>/?'''
def get_char_data(c):
im = Image.new('L',(w, h),255)
draw = ImageDraw.Draw(im)
font = ImageFont.truetype(fontpath, fontsize)
draw.text((0,0), c, font = font)
#im.show()
ans = 0.0
for i, j in product(range(w), range(h)):
ans += im.getpixel((i,j))
return ans / (255.0 * w * h)
lst = map(lambda c: [c, get_char_data(c)], charlist)
lst.sort(key=lambda i: i[1])
return lst
然后把要转换的图片转成灰度, 因为每个字符的宽长比大约是1/2, 所以图片的宽度要先伸展2倍, 然后缩小的一个需要的大小, 用每个像素的灰度值索引到之前算出的列表中的相应字符, 输出即可.
import Image
from pre import get_data_list
from itertools import product
clst = get_data_list()
im = Image.open('stevejobs.png')
size = list(im.size)
size[0]=size[0]/0.5
width = 70
size = (width,int(size[1]/size[0]*width))
im = im.resize(size)
im = im.convert('L')
#im.show()
fo = file('asciiart.txt','w')
for j in range(size[1]):
for i in range(size[0]):
idx = int( im.getpixel((i,j)) / 255.0 * (len(clst)-1) )
fo.write(clst[idx][0])
fo.write('\n')
fo.close()
效果图:
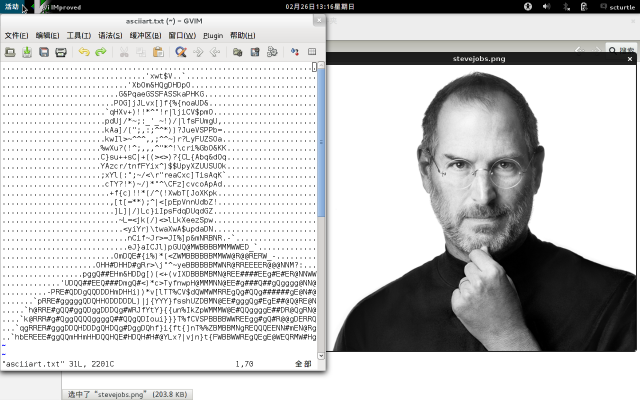
离远点看, 还是有点意思的~
